|
|
||
| Home | Login | Schedule | Pilot Store | 7-Day IFR | IFR Adventure | Trip Reports | Blog | Fun | Reviews | Weather | Articles | Links | Helicopter | Download | Bio | ||
 Site MapSubscribePrivate Pilot Learn to Fly Instrument Pilot 7 day IFR Rating IFR Adventure Commercial Pilot Multi-Engine Pilot Human Factors/CRM Recurrent Training Ground Schools Articles Privacy Policy About Me Keyword:  |
Chapter 8. HELICOPTER PERFORMANCE Assuming that a helicopter engine and all components are operating satisfactorily, the performance of the helicopter is dependent on three major factors:
Air, like liquids and other gases, is a fluid. Because it is a fluid, it flows and changes shape under pressure. Air is said to be "thin" at high altitudes; that is, there are fewer molecules per cubic foot of air at 10,000 feet than at sea level. The air at sea level is "thin" when compared to air compressed to 30 pounds of pressure in an automobile tire. A cubic inch of air compressed in an automobile tire is denser than a cubic inch of "free" air at sea level. For example, in a stack of blankets, the bottom blanket is under pressure of all blankets above it. As a result of this pressure, the bottom blanket may be squeezed down until it is only one-tenth as bulky as the fluffy blanket on top. There is still just as much wool in the bottom blanket as there is in the one on top, but the wool in the bottom blanket is 10 times more dense. If the second blanket from the bottom of the stack were removed, a force of 15 pounds might be required to pull it out. The second blanket from the top may require only 1 pound of force. In the same way, air layers near the earth's surface have much greater density than air layers at higher altitudes. The lower the elevation of the earth's surface, the greater the density of the air layers. For example, the layer of air at sea level would be denser than the layer of air at the earth's surface at Denver, Colo., at approximately 1 mile above sea level. The above principle may be applied in flying aircraft. At lower levels the rotor blade is cutting through more and denser air, which offers more support (lift) and increases air resistance. The same amount of power, applied at higher altitudes where the air is thinner and less dense, propels the helicopter faster.  Density altitude Density altitude refers to a theoretical air density which exists under standard conditions of a given altitude. Standard conditions at sea level are:
Figure 51 (above right) shows a density altitude chart. If we locate the +5C° vertical line along the bottom of the chart, follow this line up to its intersection with the 5,000-foot diagonal line, then follow the horizontal line to the left side of the chart, we read a density altitude of 5,000 feet. 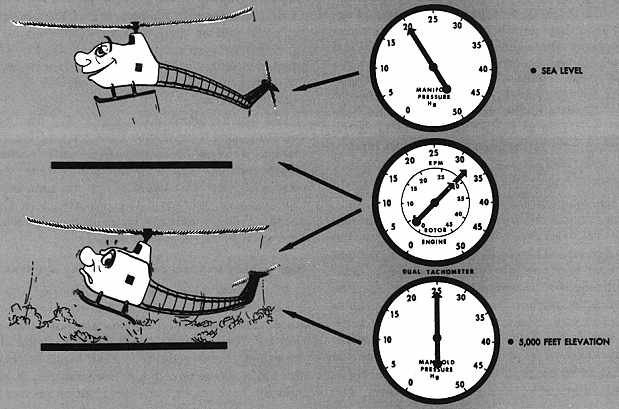 The
four factors which affect density altitude are altitude, atmospheric pressure, temperature, and moisture content of the
air. Altitude We have already seen the effects of altitude on air density in the first section of this chapter. The greater the elevation of an airport or landing area, the less the atmospheric pressure and, consequently, the less dense the air. The less dense the air, the greater the density altitude. What is the result when operating at a high density altitude? Helicopter performance is decreased (see figure 52 to the right). It can be seen from the density altitude chart that, as altitude increases, density altitude increases. Atmospheric pressure The atmospheric pressure at an airport or landing area at a given elevation can change from day to day - sometimes a very noticeable amount which, when combined with other factors, could be significant. The lower the pressure at a given elevation, the less dense the air; the less dense the air, the higher the density altitude and, as a result, the less performance the helicopter will have. The daily and seasonal variations in atmospheric pressure at a given place will not have as significant effect on the density altitude as the daily and seasonal variations of temperature and moisture. The density altitude chart is based on pressure altitude, not indicated altitude (see figure 51 above). To determine the pressure altitude at any given place, if an altimeter is available, adjust the altimeter setting to 29.92 and read the pressure altitude directly from the altimeter. However, do not forget to reset the altimeter to the current altimeter setting if available, or to field elevation if an altimeter setting is not available.  Temperature Even when elevation and pressure remain constant, great changes in air density will be caused by temperature changes. The same amount of air that occupies 1 cubic inch at a low temperature will expand and occupy 2, 3, or 4 cubic inches as the temperature rises. Therefore, as temperature increases, air becomes less dense, density altitude is increased, and the helicopter performance decreases (see figure 53 to the right). A study of figure 51 easily reveals that, as temperature increases, density altitude increases since the pressure altitude lines slope upward to the right. We have already used the density altitude chart to find the density altitude at an elevation of 5,000 feet under standard atmospheric conditions for that elevation - that is, atmospheric pressure (reduced to sea level) 29.92 inches of mercury, temperature 41.5° F. (50 C.). When the atmospheric pressure, reduced to sea level at a given elevation, is 29.92, the pressure altitude is the same as the given elevation. What would be the density altitude at this same elevation if the pressure altitude is still 5,000 feet but the temperature is 95° F. (35° C.)? Locate the 35° vertical line at the bottom of the chart (figure 51), follow this line up to its intersection with the 5,000-foot pressure altitude (diagonal) line, then move horizontally to the left side of the chart where a density altitude of 8,400 feet is read. A helicopter operating at this elevation under these conditions would be flying in air with a density equivalent to that at the 8,400-foot level. Therefore, the performance of the helicopter would be as though it were flying at the 8,400-foot level rather than the 5,000-foot level.  Moisture When temperature and pressure are constant, changes in the moisture content of the air will change air density. Water vapor weighs less than dry air. Therefore, as the moisture content of the air increases, air becomes less dense; density altitude is increased with a resultant decrease in helicopter performance (see figure 54 to the right). The higher the temperature the greater the amount of moisture the air can hold. Relative humidity, which is expressed as a percent, is the ratio of the amount of moisture in the air to the amount it is capable of absorbing at a given temperature. The moisture content of the air at a relative humidity of 80 percent and a temperature of 100° F. will be much greater than with a relative humidity of 80 percent and a temperature of 50° F. The greatest decrease in air density (increase in density altitude) due to moisture content will be at a high temperature. The density altitude chart (figure 51) does not take the moisture content of the air into consideration. It should be remembered that the actual density altitude can be much higher than that computed from this chart if the air contains a high moisture content. The importance of this added effect of moisture on helicopter hovering performance will be seen shortly. High density and low density altitude conditions The terms "high density altitude" and "low density altitude" should be thoroughly understood. In general, high density altitude refers to thin air; low density altitude refers to dense air. Therefore, those conditions that result in thin air - high elevations, high temperatures, high moisture content, or some combination thereof - would be referred to as high density altitude conditions; those conditions that result in dense air - low elevations, low temperatures, low moisture content, or some combination thereof - would be referred to as low density altitude conditions. It is important to note that high density altitudes may be present at low elevations on hot days with high moisture content in the air. 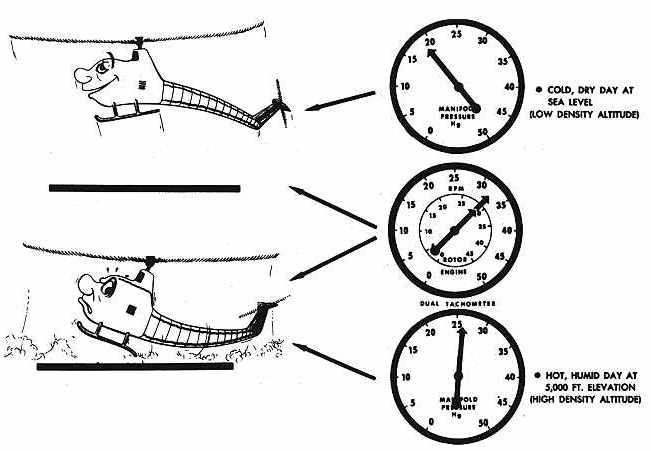 EFFECT OF
HIGH DENSITY ALTITUDES ON HELICOPTER PERFORMANCE High elevations, high temperatures, and high moisture content, all of which contribute to a high density altitude condition, lessen helicopter performance. Because the difference between the power available and the power required is so small for a helicopter, particularly in hovering flight, density altitude is of even greater importance to the helicopter pilot than it is to the airplane pilot. Helicopter performance is reduced because the thinner air at high density altitudes reduces the amount of lift of the rotor blades. Also, the (unsupercharged) engine does not develop as much power because of the thinner air and the decreased atmospheric pressure. Hovering flight High density altitudes reduce the hovering capabilities of the helicopter (see figure 55 above). Under any given load condition, the higher the density altitude, the lower the hovering ceiling; that is, the elevation at which the helicopter will be able to hover will be lowered as the density altitude increases. 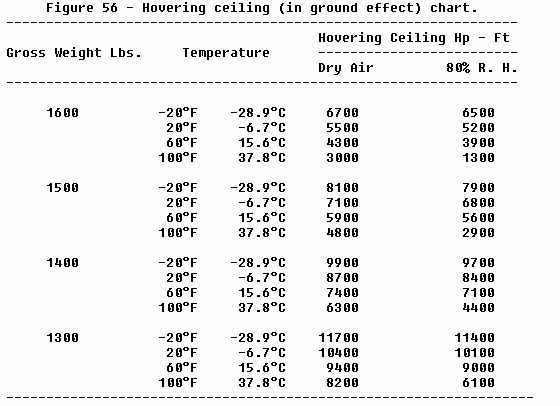 Figure 56 gives the hovering ceiling in
ground effect for one helicopter at various gross weights and
temperatures both in dry air and air at 80 percent relative humidity.
The following previously established points should be easily recognized
from this chart: 1. An increase in temperature decreases the hovering ceiling - For example, at 1,600 pounds gross weight in dry air, as the temperature increases from -20° F. to 100° F., the hovering ceiling decreases from 6,500 feet to 1,300 feet. 2. As the amount of moisture in the air increases, the hovering ceiling decreases - For example, at 1,600 pounds gross weight and 100° F., as the moisture content changes from dry air to 80 percent relative humidity, the hovering ceiling decreases from 3,000 feet to 1,300 feet; at 1,600 pounds and 20° F., as the moisture changes from dry air to 80 percent relative humidity, the hovering ceiling decreases from 5,500 feet to only 5,200 feet.  3. The higher the temperature, the greater
the amount of moisture which the air can hold - At 1,600 pounds gross
weight, and temperatures of -20° F., 20° F., 60° F., and
100° F., the change in hovering ceiling from dry air to 80 percent
relative humidity is 200 feet, 300 feet, 400 feet, and 1,700 feet,
respectively. This indicates that the amount of moisture in the air at
100° F. and 80 percent relative humidity is much greater than the
amount present at 60° F. and below. Figure 57 (right) illustrates the hovering ceiling in ground effect for temperature and gross weight variations for one helicopter, but does not reflect the effect that moisture content has on the performance. For example, at a gross weight of 1,550 pounds and a temperature of 100° F., the hovering ceiling is a pressure altitude of 4,100 feet. Takeoff For any given gross weight, the higher the density altitude at point of departure, the more power that is required to make a vertical takeoff to a hover (see figure 55 above). In fact, under certain gross weight and density altitude conditions, a helicopter may not have sufficient power to lift off vertically, in which case, if takeoff is made, it would have to be a running takeoff. 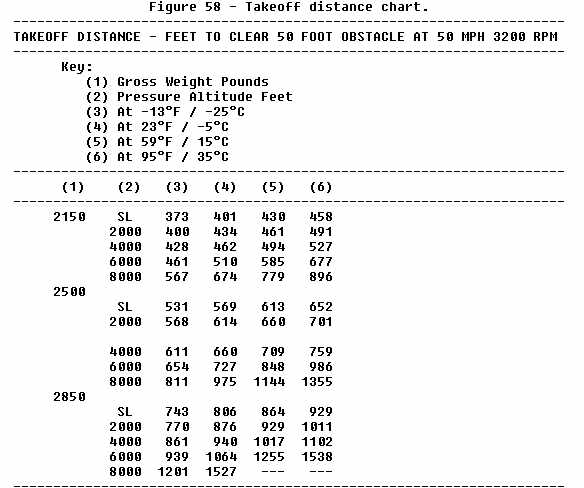 Figure 58 (right) shows a chart that is used
to compute the takeoff distance required to clear a 50-foot obstacle
under various gross weight, pressure altitude, and temperature
conditions. A brief study of the chart immediately reveals the
previously established points, that is, as gross weight, altitude, and
temperature increase, the takeoff performance decreases. This chart is
used in the following way:
SOLUTION: 1. In the first column, locate 2,500. 2. In the second column opposite 2,500, locate 6,000. 3. Follow this 6,000 row out to the column headed by 59° F. where you read 848. 4. The distance required to clear a 50-foot obstacle under these conditions then is 848 feet. Sample Problem 2 - What distance is required to clear a 50-foot obstacle if the helicopter gross weight is 2,850 pounds, the pressure altitude is 5,000 feet, and the temperature is 95° F.? The solution requires interpolation. SOLUTION: 1. In the first column, locate 2,850. 2. In the second column opposite 2,850, locate the 4,000- and 6,000-foot rows. 3. Follow each of these rows out to the column headed by 95° F., where you read 1,102 and 1,538, respectively. 4. Since 5,000 feet falls midway between 4,000 and 6,000, we assume that the takeoff distance at this altitude falls midway between 1,102 and 1,538. 5. By taking half of the difference of the two distances and adding it to 1,102 (or subtracting it from 1,538), the distance required to clear a 50-foot obstacle under the conditions of the problem is 1,320 feet. Since this chart does not take into consideration the decrease in air density due to moisture content, takeoff distances may be even greater than those computed from the table.  Rate of
climb For any given gross weight, the higher the density altitude, the less the rate of climb for any helicopter. Although a helicopter may be able to take off and clear obstacles close by, higher obstacles farther away may not be cleared because of this reduced rate of climb. Figure 59 illustrates the type of chart that is used to compute the rate of climb for one model of helicopter. The steps for using this chart are exactly the same as those listed previously for the takeoff distance chart. Figure 60 (right) illustrates another type of chart used to compute rate of climb for another model helicopter. To use this chart, you must follow these steps: 1. Compute the density altitude at the departure point using the density altitude chart (figure 51). 2. Locate this density altitude along the left side of the chart (figure 60). 3. Follow this altitude line horizontally until it intersects the diagonal line. 4. From this point of intersection, move vertically downward to the bottom of the chart where you read the rate of climb under the existing conditions. From the chart to the right in figure 60 (right), you can determine the best rate of climb airspeed under the various density altitude conditions. From the density altitude at the left side of the chart, move horizontally across until the line intersects the diagonal line on the right-hand chart. From this point of intersection, move vertically downward to the bottom of the chart where you will read the best rate of climb speed in miles per hour.  Landing Because a pilot can hover at a takeoff point with a certain gross weight, it does not mean that hovering power will be available at the destination airport. If the destination is at a higher altitude and/or higher temperature and moisture content prevail, sufficient power may not be available to hover at the destination with the existing gross weight. The pilot will have to make a running landing under these conditions. The pilot should be able to predict whether hovering power will be available at the destination through (1) a knowledge of temperature, relative humidity, and wind conditions, (2) the use of charts in the helicopter flight manual such as figures 56 and 57, and (3) by making certain power checks in flight prior to attempting to land. These power checks will be discussed later. The illustration to the right is a typical chart that is used to compute the total landing distance over a 50-foot obstacle for one model of helicopter. The steps for using this chart are exactly the same as those listed previously for the takeoff distance chart. Notice that the total landing distance does not vary as much as the total takeoff distance (fig. 58 above) with equal variations in gross weight, altitude, or temperature. These charts apply to the same helicopter. Your Thoughts... |
|
| Home | Login | Schedule | Pilot Store | 7-Day IFR | IFR Adventure | Trip Reports | Blog | Fun | Reviews | Weather | Articles | Links | Helicopter | Download | Bio |
| All content is Copyright 2002-2010 by Darren Smith. All rights reserved. Subject to change without notice. This website is not a substitute for competent flight instruction. There are no representations or warranties of any kind made pertaining to this service/information and any warranty, express or implied, is excluded and disclaimed including but not limited to the implied warranties of merchantability and/or fitness for a particular purpose. Under no circumstances or theories of liability, including without limitation the negligence of any party, contract, warranty or strict liability in tort, shall the website creator/author or any of its affiliated or related organizations be liable for any direct, indirect, incidental, special, consequential or punitive damages as a result of the use of, or the inability to use, any information provided through this service even if advised of the possibility of such damages. For more information about this website, including the privacy policy, see about this website. |